|
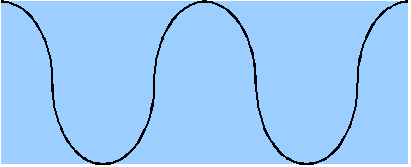
これらは、ある長さの伝送線路に信号を通した場合の、電圧分布を図にしたものです。両者の間で異なるのは、使用する信号の周波数だけだとします。波長は周波数に反比例するので、図(b)に示した信号は、図(a)に比べて、周波数が高い信号です。
さて、これらの信号の電圧についてみてみましょう。図(a)では、どの場所でも電圧はほぼ一定の値になっていますが、図(b)では、どの場所でモニタリングするかによって、電圧値が異なってくることがお分かりいただけるでしょうか。
取り扱う周波数が急に高くなると、このような分布を考慮に入れて設計を行わなくてはいけなくなってくるため、今まで経験したことがないような現象に遭遇するようになってくるのです。
これらの線路を回路的に見てみると、図(a)では、どの場所でも電圧が一定であるため、一つの素子とみなすことが出来ます。このような考え方を集中定数回路と呼びます。
一方、図(b)では、場所により電圧が異なってくるため、伝送線路も、微小な素子が連なって一つの回路を形成していると考える必要があります。このような考え方を、微小な素子が分布している、ということから分布定数回路と呼びます。
これまで見てきたように、伝送線路に対して信号の波長が短い場合、線路の長さを考慮する必要がでてきます。一般的には、伝送線路の長さが、波長の4分の1より長い場合、分布乗数の考え方をしなくてはならない、と言われる場合が多いようです。
次回は、分布定数回路について、もう少し詳しく説明します。 |